MECÂNICA GENERALIZADA GRACELI - QUÂNTICA QUÍMICA RELATIVISTA [22]

Quantidades equivalentes usadas na teoria de espalhamento de espécimes compostos, mas com uma variedade de unidades.

Quando um alvo é um conjunto de vários centros espalhadores cujas posições relativas variam de forma imprevisível, é costumeiro que se pense em uma equação de alcance cujos argumentos tomem diferentes formas em diferentes áreas de aplicação. O caso mais simples considera uma interação que remove partículas de um "feixe não espalhado" a uma taxa uniforme que é proporcional ao fluxo incidente $I$ de partículas por unidade de área por unidade de tempo, ou seja, que

{\frac {dI}{dx}}=-QI\,\!

G ψ = E ψ = E

\lambda

ψ ω Mom=

\,N_{A}

\,M

\,z^{+}

\,z^{-}

\,e

\,\epsilon _{o}

] /

\,r_{0}

/ =

\lambda

ħω

q\ \

[Ϡ ] [ξ ] [,ς]

g_{s}

\epsilon _{s}

{\vec {A}}\ \

{\begin{pmatrix}\psi _{0}\\\psi _{1}\end{pmatrix}}

ψ μ / h/c ψ(x, t)

-i\hbar {\frac {\partial }{\partial x_{n}}}

x t ]..

onde "Q" é um coeficiente de interação e "x" é a distância viajada no alvo.

A equação diferencial ordinária de primeira ordem acima tem soluções da forma:

I=I_{o}e^{-Q\Delta x}=I_{o}e^{-{\frac {\Delta x}{\lambda }}}=I_{o}e^{-\sigma (\eta \Delta x)}=I_{o}e^{-{\frac {\rho \Delta x}{\tau }}},

G ψ = E ψ = E

\lambda

ψ ω Mom=

\,N_{A}

\,M

\,z^{+}

\,z^{-}

\,e

\,\epsilon _{o}

] /

\,r_{0}

/ =

\lambda

ħω

q\ \

[Ϡ ] [ξ ] [,ς]

g_{s}

\epsilon _{s}

{\vec {A}}\ \

{\begin{pmatrix}\psi _{0}\\\psi _{1}\end{pmatrix}}

ψ μ / h/c ψ(x, t)

-i\hbar {\frac {\partial }{\partial x_{n}}}

x t ]..

onde I_o é o fluxo inicial, comprimento de caminho Δx ≡ x − x_o, a segunda igualdade define uma interação de livre caminho médio λ, a terceira usa o número de alvos por unidade de volume, η, para definir uma área de seção de choque σ, e a última usa a densidade de massa do alvo, ρ, para definir uma densidade de livre caminho médio, τ. Dessa forma, podemos relacionar essas quantidades por meio de Q = 1/λ = ησ = ρ/τ, como mostrada na figura à esquerda.

A intensidade I da luz dispersada por uma pequena partícula num feixe de luz de comprimento de onda λ e intensidade I₀ é dada por:

I=I_{0}\,{\frac {1+\cos ^{2}\theta }{2\,R^{2}}}\left({\frac {2\pi }{\lambda }}\right)^{4}\left({\frac {n^{2}-1}{n^{2}+2}}\right)^{2}\left({\frac {d}{2}}\right)^{6}

G ψ = E ψ = E

\lambda

ψ ω Mom=

\,N_{A}

\,M

\,z^{+}

\,z^{-}

\,e

\,\epsilon _{o}

] /

\,r_{0}

/ =

\lambda

ħω

q\ \

[Ϡ ] [ξ ] [,ς]

g_{s}

\epsilon _{s}

{\vec {A}}\ \

{\begin{pmatrix}\psi _{0}\\\psi _{1}\end{pmatrix}}

ψ μ / h/c ψ(x, t)

-i\hbar {\frac {\partial }{\partial x_{n}}}

x t ]..

Onde R é a distância à partícula, θ é o ângulo de dispersão, n é o índice de refração da partícula e d é o diâmetro da partícula.

No caso de luz polarizada (e não se pode generalizar) também podemos expressar:

I=I_{0}\,|\sigma (\theta ,\phi )|^{2}\,{\frac {(2\pi )^{2}}{(\lambda R)^{2}}}

G ψ = E ψ = E

\lambda

ψ ω Mom=

\,N_{A}

\,M

\,z^{+}

\,z^{-}

\,e

\,\epsilon _{o}

] /

\,r_{0}

/ =

\lambda

ħω

q\ \

[Ϡ ] [ξ ] [,ς]

g_{s}

\epsilon _{s}

{\vec {A}}\ \

{\begin{pmatrix}\psi _{0}\\\psi _{1}\end{pmatrix}}

ψ μ / h/c ψ(x, t)

-i\hbar {\frac {\partial }{\partial x_{n}}}

x t ]..

\sigma (\theta ,\phi )=A(\theta )\operatorname {sen} {\phi }\,{\hat {e}}_{\phi }+B(\theta )\cos {\phi }\,{\hat {e}}_{\theta }

G ψ = E ψ = E

\lambda

ψ ω Mom=

\,N_{A}

\,M

\,z^{+}

\,z^{-}

\,e

\,\epsilon _{o}

] /

\,r_{0}

/ =

\lambda

ħω

q\ \

[Ϡ ] [ξ ] [,ς]

g_{s}

\epsilon _{s}

{\vec {A}}\ \

{\begin{pmatrix}\psi _{0}\\\psi _{1}\end{pmatrix}}

ψ μ / h/c ψ(x, t)

-i\hbar {\frac {\partial }{\partial x_{n}}}

x t ]..

Onde agora a parte dos símbolos anteriores temos o coeficiente de dispersão σ, e os ângulos em coordenadas esféricas θ e Φ. Onde seus vetores unitários se definem referidos ao plano que definem o vetor que contém a direção de propagação da radiação e o vetor que contém a direção da polarização da onda incidente. A parte temos os coeficientes da matriz de Lennard-Jones perpendicular A(θ) e paralelo B(θ) ao plano de dispersão.

A distribuição angular da dispersão de Rayleigh, que vem a ser dada pela fórmula (1+cos²θ), é simétrica no plano perpendicular à direção da luz incidente, portanto a luz dispersada iguala-se à luz incidente. Integrando a área da esfera que cerca una partícula obtemos a seção de choque da dispersão de Rayleigh, σ_s:

\sigma _{s}={\frac {2\pi ^{5}}{3}}{\frac {d^{6}}{\lambda ^{4}}}\left({\frac {n^{2}-1}{n^{2}+2}}\right)^{2}

G ψ = E ψ = E

\lambda

ψ ω Mom=

\,N_{A}

\,M

\,z^{+}

\,z^{-}

\,e

\,\epsilon _{o}

] /

\,r_{0}

/ =

\lambda

ħω

q\ \

[Ϡ ] [ξ ] [,ς]

g_{s}

\epsilon _{s}

{\vec {A}}\ \

{\begin{pmatrix}\psi _{0}\\\psi _{1}\end{pmatrix}}

ψ μ / h/c ψ(x, t)

-i\hbar {\frac {\partial }{\partial x_{n}}}

x t ]..

O coeficiente de dispersão para um grupo de partículas é o número de partículas por unidade de volume N vezes a seção transversal. Como em todos os efeitos de onda, na dispersão incoerente as potências são somadas aritmeticamente, ainda que na dispersão coerente (como acontece quando as partículas estão muito próximas umas das outras) os campos são somados aritmeticamente e a soma deve ser elevada ao quadrado, para obter a potência final.

Em física, a dispersão de Rutherford é um fenômeno que foi explicado por Ernest Rutherford em 1909,^[1] e levou ao desenvolvimento da teoria orbital do átomo. É agora explorado pela técnica de análise de materiais espectrometria de dispersão de Rutherford. A dispersão de Rutherford é também referida às vezes como dispersão de Coulomb porque baseia-se em forças eletrostáticas (Coulomb). Um processo similar provou o interior do núcleo nos anos 1960, chamado dispersão profunda inelástica.

Destaques da experiência de Rutherford

Um feixe de partículas alfa é direcionado a uma folha de ouro fina.
Muitas das partículas passaram através da película sem sofrer desvio.
Outras foram desviadas por diversos ângulos.
Algumas inverteram o sentido do movimento.

A partir destes resultados, Rutherford concluiu que a maioria da massa era concentrada numa região minúscula, positivamente carregada (o núcleo), rodeada por electrões. Quando uma partícula alfa (positiva) se aproximava o suficiente do núcleo, era fortemente repelida.^[2] O pequeno tamanho do núcleo explicou a pequena quantidade de partículas alfa que foram repelidas em ângulos maiores. Rutherford demonstrou usando o método abaixo, que o tamanho do núcleo era inferior do que cerca de $\scriptstyle 10^{-14}$

Teoria de Dispersão

Geometria de dispersão de Rutherford.

Principais pressupostos:

• Colisão entre uma carga pontual, mais um núcleo pesado com carga Q=Ze é um projétil leve com carga q=ze é considerada como sendo elástica.

• Momento e energia são conservados.

• As partículas interagem através da força de Coulomb.

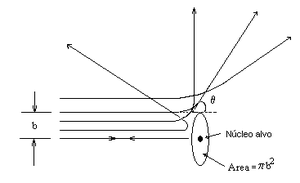
• A distância vertical onde o projétil se encontra a partir do centro do alvo, o parâmetro de impacto b , determinam o ângulo de dispersão θ.

A relação entre o ângulo de dispersão θ, a energia cinética inicial

$E=z{\frac {1}{2}}m.v_{o}^{2}$ G ψ = E ψ = E $\lambda$ ψ ω Mom= $\,N_{A}$ $\,M$ $\,z^{+}$ $\,z^{-}$ $\,e$ [/ $\,\epsilon _{o}$ ] / $\,r_{0}$ / = $\lambda$ ħω $q\ \$ [Ϡ ] [ξ ] [,ς] $g_{s}$ $\epsilon _{s}$ ${\vec {A}}\ \$ ${\begin{pmatrix}\psi _{0}\\\psi _{1}\end{pmatrix}}$ ψ μ / h/c ψ(x, t) $-i\hbar {\frac {\partial }{\partial x_{n}}}$ x t ]..

e o parâmetro de impacto b é dado pela relação

$b={\frac {zZ}{2K}}.{\frac {e^{2}}{4\pi \varepsilon _{o}}}{\text{cot}}{\Bigg (}{\frac {\theta }{2}}{\Bigg )}$ (1,1) / G ψ = E ψ = E $\lambda$ ψ ω Mom= $\,N_{A}$ $\,M$ $\,z^{+}$ $\,z^{-}$ $\,e$ [/ $\,\epsilon _{o}$ ] / $\,r_{0}$ / = $\lambda$ ħω $q\ \$ [Ϡ ] [ξ ] [,ς] $g_{s}$ $\epsilon _{s}$ ${\vec {A}}\ \$ ${\begin{pmatrix}\psi _{0}\\\psi _{1}\end{pmatrix}}$ ψ μ / h/c ψ(x, t) $-i\hbar {\frac {\partial }{\partial x_{n}}}$ x t ]..

onde z = 2, para partículas-α e Z = 79 de ouro.

Dedução da Transversal Diferencial

Na Figura , uma partícula que atinge o anel entre b e b + db é desviada num ângulo sólido dΩ entre θ e θ + dθ.

Por definição, a secção transversal é a constante de proporcionalidade

$2\pi b.db=-\sigma (\theta ).2\pi .\operatorname {sen} \theta .d\theta$

então

$d\sigma =2\pi b|db|={\Bigg (}{\frac {d\sigma }{d\Omega }}{\Bigg )}.d\Omega$ (1,2) / G ψ = E ψ = E $\lambda$ ψ ω Mom= $\,N_{A}$ $\,M$ $\,z^{+}$ $\,z^{-}$ $\,e$ [/ $\,\epsilon _{o}$ ] / $\,r_{0}$ / = $\lambda$ ħω $q\ \$ [Ϡ ] [ξ ] [,ς] $g_{s}$ $\epsilon _{s}$ ${\vec {A}}\ \$ ${\begin{pmatrix}\psi _{0}\\\psi _{1}\end{pmatrix}}$ ψ μ / h/c ψ(x, t) $-i\hbar {\frac {\partial }{\partial x_{n}}}$ x t ]..

onde $d\Omega =2\pi .\operatorname {sen} \theta .d\theta$

A seção transversal diferencial torna-se então

${\frac {d\sigma }{d\Omega }}={\frac {2\pi b|db|}{2\pi .\operatorname {sen} \theta .d\theta }}$ (1,3) / G ψ = E ψ = E $\lambda$ ψ ω Mom= $\,N_{A}$ $\,M$ $\,z^{+}$ $\,z^{-}$ $\,e$ [/ $\,\epsilon _{o}$ ] / $\,r_{0}$ / = $\lambda$ ħω $q\ \$ [Ϡ ] [ξ ] [,ς] $g_{s}$ $\epsilon _{s}$ ${\vec {A}}\ \$ ${\begin{pmatrix}\psi _{0}\\\psi _{1}\end{pmatrix}}$ ψ μ / h/c ψ(x, t) $-i\hbar {\frac {\partial }{\partial x_{n}}}$ x t ]..

A partir da Equações 1,1 e 1,3 nós temos

${\frac {d\sigma }{d\Omega }}={\Bigg (}{\frac {1}{4\pi \varepsilon _{o}}}{\Bigg )}^{2}{\Bigg (}{\frac {qQ}{4K_{\alpha }}}{\Bigg )}^{2}.{\frac {1}{\operatorname {sen} ^{4}}}{\Bigg (}{\frac {\theta }{2}}{\Bigg )}$ (1.4)/ G ψ = E ψ = E $\lambda$ ψ ω Mom= $\,N_{A}$ $\,M$ $\,z^{+}$ $\,z^{-}$ $\,e$ [/ $\,\epsilon _{o}$ ] / $\,r_{0}$ / = $\lambda$ ħω $q\ \$ [Ϡ ] [ξ ] [,ς] $g_{s}$ $\epsilon _{s}$ ${\vec {A}}\ \$ ${\begin{pmatrix}\psi _{0}\\\psi _{1}\end{pmatrix}}$ ψ μ / h/c ψ(x, t) $-i\hbar {\frac {\partial }{\partial x_{n}}}$ x t ]..

A Eq.1.4, é chamada seção transversal diferencial para a dispersão de Rutherford.

Nos cálculos acima, considera-se apenas uma única partícula alfa. Num experimento de dispersão, é preciso considerar vários eventos de dispersão e medir-se a fracção de partículas desviadas num determinado ângulo.

Para um detector em um ângulo específico em relação ao feixe incidente, o número de partículas por unidade de superfície, colidindo o detector, é dado pela fórmula de Rutherford:

$N(\theta )={\frac {N_{i}.nLZ^{2}k^{2}.e^{4}}{4.r^{2}k.E^{2}\operatorname {sen} ^{4}{\Bigg (}{\frac {\theta }{2}}{\Bigg )}}}$ G ψ = E ψ = E $\lambda$ ψ ω Mom= $\,N_{A}$ $\,M$ $\,z^{+}$ $\,z^{-}$ $\,e$ [/ $\,\epsilon _{o}$ ] / $\,r_{0}$ / = $\lambda$ ħω $q\ \$ [Ϡ ] [ξ ] [,ς] $g_{s}$ $\epsilon _{s}$ ${\vec {A}}\ \$ ${\begin{pmatrix}\psi _{0}\\\psi _{1}\end{pmatrix}}$ ψ μ / h/c ψ(x, t) $-i\hbar {\frac {\partial }{\partial x_{n}}}$ x t ]..

Verificação da fórmula de Rutherford

Onde:

Ni = número de partículas alfa incidentes;

n = átomos por unidade de volume no alvo;

L = espessura do alvo;

Z = número atómico do alvo;

e = carga electrónica;

k = constante de Coulomb;

r = distância entre o alvo e o detector;

KE = energia cinética das partículas alfa;

θ = ângulo de dispersão.

A variação prevista, de partículas alfa detectadas, com ângulo é seguida de perto podados do contador de Geiger-Marsden, mostrados na Figura abaixo.

Cálculo do tamanho nuclear máximo

Espalhamento com diferentes parâmetros de impacto.

Para colisões frontais cabeças entre partículas alfa e o núcleo, toda a energia cinética $\scriptstyle E=z{\frac {1}{2}}m.v_{o}^{2}$ G ψ = E ψ = E $\lambda$ ψ ω Mom= $\,N_{A}$ $\,M$ $\,z^{+}$ $\,z^{-}$ $\,e$ [/ $\,\epsilon _{o}$ ] / $\,r_{0}$ / = $\lambda$ ħω $q\ \$ [Ϡ ] [ξ ] [,ς] $g_{s}$ $\epsilon _{s}$ ${\vec {A}}\ \$ ${\begin{pmatrix}\psi _{0}\\\psi _{1}\end{pmatrix}}$ ψ μ / h/c ψ(x, t) $-i\hbar {\frac {\partial }{\partial x_{n}}}$ x t ]..

da partícula alfa é transformada em energia potencial e a partícula está em repouso.

A distância entre o centro da partícula alfa e o centro do núcleo (b) neste momento é um valor máximo para o raio, se é evidente a partir da experiência que as partículas não atingiram o núcleo.

Aplicando a energia potencial de Coulomb entre as cargas nos electrões e no núcleo, pode-se escrever:

${\frac {1}{2}}.m.v^{2}={\frac {1}{4\pi \varepsilon _{o}}}.{\frac {q_{1}q_{2}}{b}}$ G ψ = E ψ = E $\lambda$ ψ ω Mom= $\,N_{A}$ $\,M$ $\,z^{+}$ $\,z^{-}$ $\,e$ [/ $\,\epsilon _{o}$ ] / $\,r_{0}$ / = $\lambda$ ħω $q\ \$ [Ϡ ] [ξ ] [,ς] $g_{s}$ $\epsilon _{s}$ ${\vec {A}}\ \$ ${\begin{pmatrix}\psi _{0}\\\psi _{1}\end{pmatrix}}$ ψ μ / h/c ψ(x, t) $-i\hbar {\frac {\partial }{\partial x_{n}}}$ x t ]..

Reorganizando,

${\frac {1}{4\pi \varepsilon _{o}}}{\frac {2.q_{1}q_{2}}{m.v^{2}}}$ (1,6) / G ψ = E ψ = E $\lambda$ ψ ω Mom= $\,N_{A}$ $\,M$ $\,z^{+}$ $\,z^{-}$ $\,e$ [/ $\,\epsilon _{o}$ ] / $\,r_{0}$ / = $\lambda$ ħω $q\ \$ [Ϡ ] [ξ ] [,ς] $g_{s}$ $\epsilon _{s}$ ${\vec {A}}\ \$ ${\begin{pmatrix}\psi _{0}\\\psi _{1}\end{pmatrix}}$ ψ μ / h/c ψ(x, t) $-i\hbar {\frac {\partial }{\partial x_{n}}}$ x t ]..